LeetCode1162号问题
你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

示例 1：

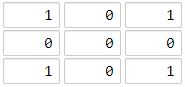
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。
示例 2：

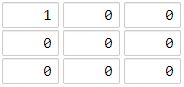
输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。
 

提示：

1 <= grid.length == grid[0].length <= 100
grid[i][j] 不是 0 就是 1

思路

1. 将每一个陆地区域，看作一个出发点，依次从这些出发点出发，进行上下左右的探寻。
2. 对于未探索过的地点，在每次探寻之后，将此位置的值在当前出发点的基础上加1。
3. 如果这个地点已经被探索过，则忽略此地点。
4. 如果某一个出发点周围已经没有任何未探索地点，则下一轮探索中，将不会再从这个出发点进行任何探索。
5. 直到没有任何可进行探索的出发点，程序结束。最后一个出发点的值-1，则代表最远距离。

Java代码实现

 public static int maxDistance(int[][] grid) {
        int[] directX = {0, 0, 1, -1};//X前进方向
        int[] directY = {1, -1, 0, 0};//Y前进方向

        Queue<int[]> queue = new ArrayDeque<>();//表示搜索起点队列
        //将所有起点添加到队列中
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == 1) {
                    queue.offer(new int[]{i, j});
                }
            }
        }
        if (queue.isEmpty()) return -1;
        int[] nowPoint = null;
        boolean ocean = false;
        while (!queue.isEmpty()) {
            nowPoint = queue.poll();//将当前出发点取出
            int nowX = nowPoint[0], nowY = nowPoint[1];
            for (int i = 0; i < 4; i++) {
                int newX = nowX + directX[i];
                int newY = nowY + directY[i];
                //如果超出边界，或者已经被探访过，则继续寻找
                if (newX < 0 || newX >= grid.length || newY < 0 || newY >= grid[0].length || grid[newX][newY] != 0) {
                    continue;
                }
                ocean = true;
                grid[newX][newY] = grid[nowX][nowY] + 1;//在出发点值的基础上+1
                queue.offer(new int[]{newX, newY});//将新探访的地区，加入到队列中
            }
        }
        if (!ocean) return -1;
        return grid[nowPoint[0]][nowPoint[1]] - 1;//最后一个出发点
    }